‘몬티홀 문제의 딜레마’, 선택을 바꾸시겠습니까?

몬티홀 문제 사회의 중대한 현상에 적용할 수 있을까?

[객원 에디터 6기/ 이지윤 기자] 1963년부터 약 40년 동안 방영한 미국의 TV 쇼 “거래를 합시다” 는 퍼즐 문제인 “몬티 홀 문제” 로 유명하다. 몬티 홀 문제는 사람들이 흔히 가지고 있는 확증 편향에 의문점을 던지고, 간단하지만 많은 사람들이 틀리는 확률문제이다. 실제 이 프로그램의 진행자 인 몬티 홀(Monty Hall)의 이름을 따서 만든 문제인 몬티 홀 문제는 다음과 같다. 

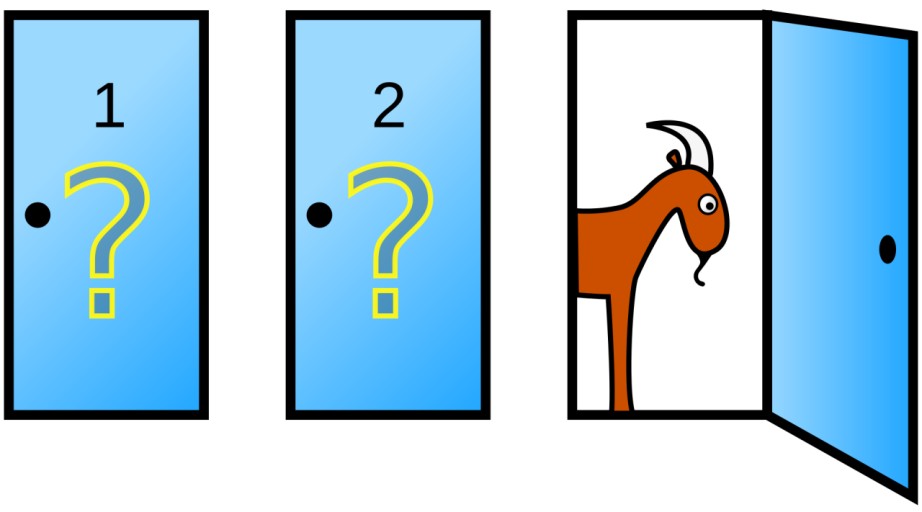
한 참가자가 게임 쇼에 참가해서 A, B, 그리고 C, 이 세 개의 문 중에서 하나를 고를 기회를 가졌다고 가정해 보자. 이 세 개의 문 중 하나의 문 뒤에는 엄청난 금액의 자동차가 있고, 나머지 두 문 뒤에는 염소가 있다. 예를 들어 참가자가 A 문을 선택하면, 진행자는 참가가 고르지 않은 두 문, 즉 B와 C문 중에서 자동차가 없는 문이 무엇인지 알려준다. 만약 C 문이 염소가 있는 문이라고 가정하면, 진행자는 C 문을 열어 자동차가 없음을 참가자에게 보여준 뒤, 참가자에게 “A 문에 남아계시겠습니까? 아니면 B문으로 바꾸시겠습니까?”라고 질문을 던진다. 이런 경우에서 선택을 바꾸는 것이 이득일까?

이 질문에 대해 많은 사람들은 선택을 바꾸지 않는다고 대답한다. 두 개의 문 중에서 하나의 문 뒤에 자동차가 있기 때문에 A문을 고르던 B문을 고르던 자동차를 가질 확률이 ½ 로 동일하다고 생각하기 때문이다. 이러한 추론 방식 때문에 사람들은 오히려 선택지가 두 개의 문으로 줄어들면 차를 가질 확률이 차가 3개 있을 때 차를 가질 확률인 ⅓ 에서 차가 2개 있을 때의 확률인 ½ 로 증가한다고 생각하고, 문을 바꾸지 않는 것이 더 이득이라고 생각한다. 

하지만 통계학적으로 많은 사람들이 생각하는 선택은 잘못되었다. 즉, 문 A에서 문 B로 바꾸는 것이 차를 가질 수 있는 확률을 높인다는 것이다. 왜 그런 것일까? 

예를 들어, 참가자가 문 A 를 선택한 경우, 

문 A뒤에 차가 있을 확률= ⅓ 

문 B 나 문 C 뒤에 차가 있을 확률=⅔이다.

이런 상황에서 진행자가 문 C를 열어 문 C뒤에 차가 아닌 염소가 있음을 보여주면, 참가자는 당연히 문 C를 선택하지 않게 되고, 문 C뒤에 차가 있을 확률은 0 이 된다. 따라서 문 B 나 문 C 뒤에 차가 있을 확률= 문 B뒤에 차가 있을 확률 + 문 C뒤에 차가 있을 확률 이기 때문에 C의 확률이 0이 되면 문 B 나 문 C 뒤에 차가 있을 확률= 문 B뒤에 차가 있을 확률=⅔이라는 결론이 도출된다. 

이 몬티홀 문제는 알고 보면 간단하지만 인간의 직관과 대조되기 때문에 많은 사람들이 아직까지도 쉽게 이해하지 못하는 문제 중 하나이다. 실제로 1990년에 몬티홀 문제의 정답이 ⅔이라고 제시한 최고 IQ보유자 메릴린 사반트는 사람들이 정답이 ⅔이라는 사실을 받아들이지 못해 많은 항의 편지를 받았다고 한다. 또한 이 문제는 확률적인 ‘이론’에만 집중하기 때문에 코로나 바이러스나 4차 산업혁명과 같은 사회의 중대한 주제에 적용시키기에는 위험 부담이 크다. 사회에서 발생하는 상황들은 다양한 변수를 포함하기 때문에 몬티홀 문제의 조건들이 모두 성립하지 않을 확률이 크기 때문이다.